[最も選択された] 並べ方 と 組み合わせ 方 問題 106571-6年生 並べ方 と 組み合わせ 方 問題
リーグ戦とトーナメント戦 小学校６年教材より 身勝手な主張
がら「組み合わせ」について説明し，「並べ方」と「組み合わせ」が用いられる場合それぞれについて判断す ることができる。 (2)本時の展開（4／6） 学習活動 児童の姿 教師の働きかけ・発問 手立てならべ方・組み合わせの問題の解き方 では例にも挙げた2つの問題をそれぞれ解いていきます。 （1）3人の中からリレーの 第一走者 と 第二走者 をそれぞれ選ぶ時、何通りが考えられるか。 （2）3人の中からリレーの 走者を2名 選ぶ時、何通りが考えられるか。 （1）ならべ方の問題の解き方 （1）のように選んで順番をつける場合の数の問題は、『ならべ方』の問題です。 このような
6年生 並べ方 と 組み合わせ 方 問題
6年生 並べ方 と 組み合わせ 方 問題-小学6年生の算数 場合の数｜組み合わせ 練習問題プリント ツイート 順序は考えず選んで組を作るときの選び方 「組み合わせ」を調べる方法を練習できる問題プリントです。 場合の数・組み合わせ（1） 答え 場合の数・組み合わせ（2） 答え 場合1 単元名 並べ方と組み合わせ方 2 単元について （1）単元観 本単元は、学習指導要領には以下のように位置づけられている。 目標 （d 数量関係） d（5）起こりえる場合
高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ
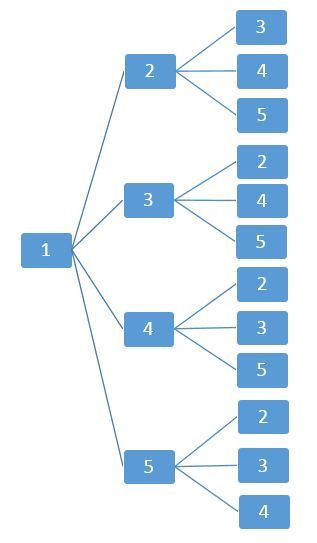
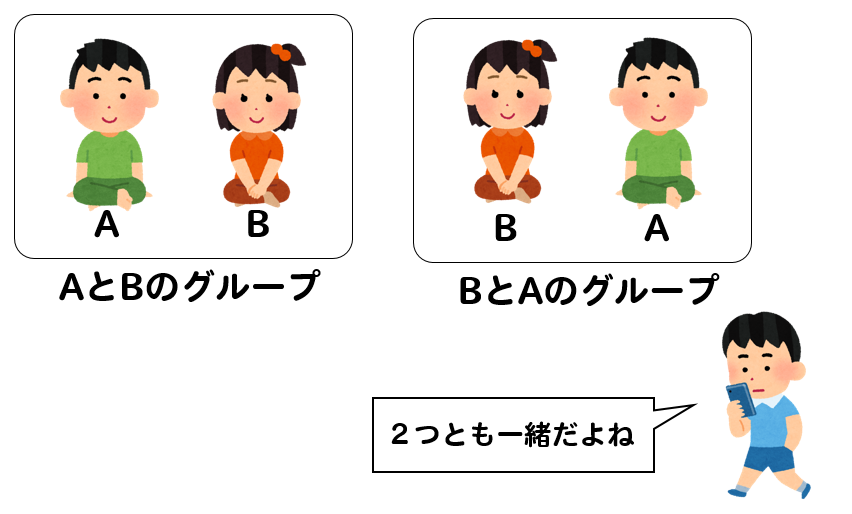
組み合わせの基本例）a,b,c,d,e の5人の中から2人ずつ組みになる作り方は何通りありますか。樹形図を書いて考える並べ方と違って ab 、ba は同じ組み合わせになるので、重ならないように書いて考えます。10通り計算で考える5×4＝通り ←2人選ぶ並べ方ab と 順列と組み合わせの概要・公式・違い 順列と組み合わせの計算方法は記事の後半に回して、まずは 順列と組み合わせとは何なのか、その2つの違い も含めて紹介します。 順列とは、いくつかのものを順序をつけて列に並べる 並べ方 の総数です。順列とは、順序を持った並べ方。例えば、{1,2}と{2,1}は別のもの。 組み合わせは、順序を持たない並べ方。例えば、{1,2}と{2,1}は同じもの。 例題(順列・組み合わせの基本) 1から3までの数が書かれたカードを2回引きます。そして、1回目と2回目に何を引いたか
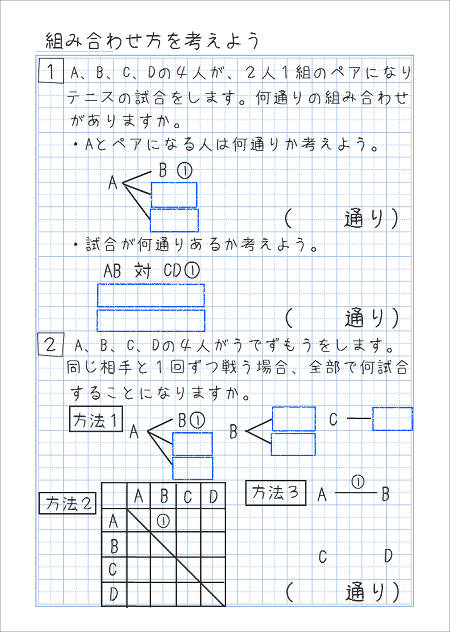
小学校 6年生 算数 かく力を高める問題 一括ダウンロード 文字と式 解答 分数のかけ算 解答 比 解答 角柱と円柱の体積 解答 並べ方と組み合わせ方 解答 データの調べ方 解答 たしかめ問題1 解答 たしかめ問題2 解答ならない取り出し方の場合は組合せで考えればいいわけです。 では、問題を考えてみましょう。 1 (1)は「第1走者から第4走者までの4人を選ぶ・・・」 つまり、順序が問題になるので、『順列』の考えで。 4は「男子6人、女子10人の中から男子3人、女子4人順列の問題（ならべ方）1 (1)男子2人に女子3人でリレーの順番を決めます。 ①全部で何通りの順番がありますか。 ②男子と女子が交互になる順番は何通りありますか。 （2）0 1 2 3の4枚のカードから3枚を並べて3けたの整数を作ります。 ①全部で何通りの整数ができますか。
6年生 並べ方 と 組み合わせ 方 問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
「6年生 並べ方 と 組み合わせ 方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
「6年生 並べ方 と 組み合わせ 方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ | 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ | 試合の組合せ 算数嫌い0 ゼロ 先生のブログ | 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
「6年生 並べ方 と 組み合わせ 方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ | 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ | 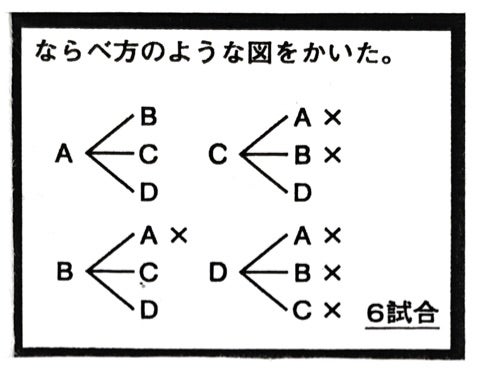 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
「6年生 並べ方 と 組み合わせ 方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ | 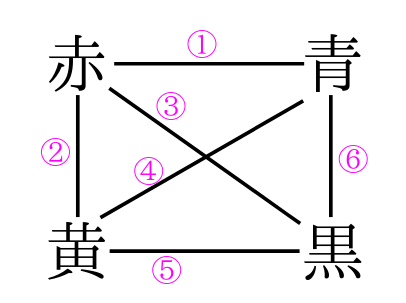 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ | 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
「6年生 並べ方 と 組み合わせ 方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
「6年生 並べ方 と 組み合わせ 方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ | 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ | 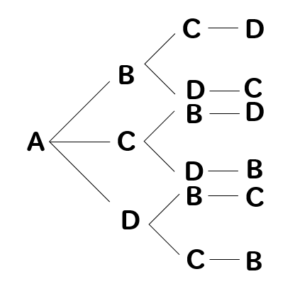 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
「6年生 並べ方 と 組み合わせ 方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ | 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |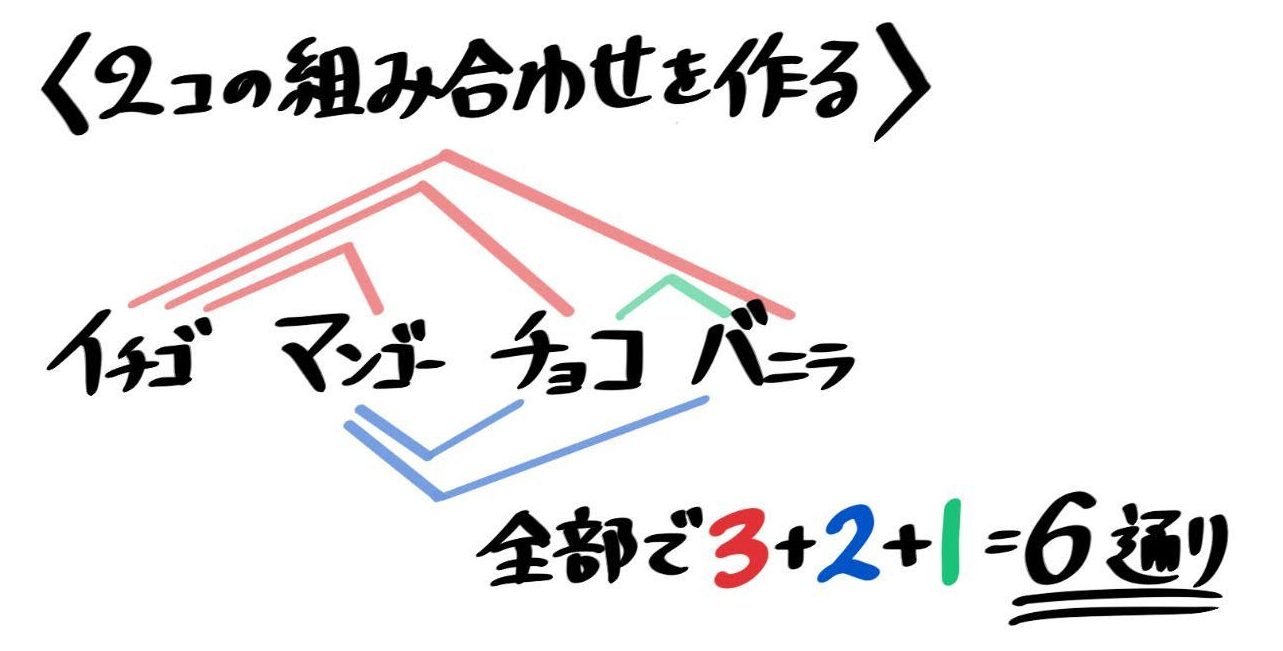
試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
「6年生 並べ方 と 組み合わせ 方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ | 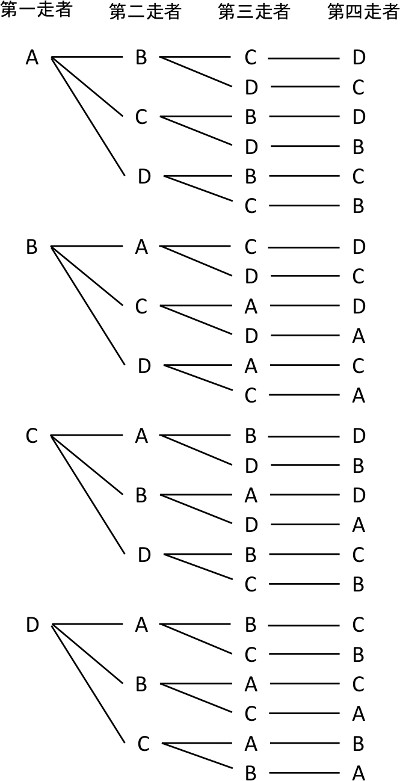 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
「6年生 並べ方 と 組み合わせ 方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ | 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ | 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
「6年生 並べ方 と 組み合わせ 方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
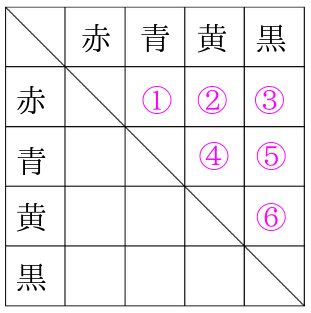 試合の組合せ 算数嫌い0 ゼロ 先生のブログ | 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
「6年生 並べ方 と 組み合わせ 方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
 試合の組合せ 算数嫌い0 ゼロ 先生のブログ |  試合の組合せ 算数嫌い0 ゼロ 先生のブログ |
小学校6年生算数学期タイトルダウンロードファイル1学期1 対称な図形2 文字と式3 分数と整数のかけ算・わり算4 分数の 場合の数の単元の順列(並べ方)の問題が苦手な小学生への教え方 場合の数における順列(並べ方)というのは、人や物などを並べるということです。 例えば3人の人を並べるようなことをいいます。 それでは、例題と用いて場合の数、順列(並べ方)の数え方を
Incoming Term: 6年生 並べ方 と 組み合わせ 方 問題,
